Patrick Lin

I work at Google. Previously, I obtained my PhD in Computer Science from the University of Illinois Urbana-Champaign (UIUC), where I was advised by Jeff Erickson. My CV: pdf.

☆Want to chat? Feel free to schedule a meeting.☆

Recent Updates

Teaching

During my time at UIUC, I primarily taught courses related to Algorithms and Theoretical CS, though I am broadly interested in teaching anything I am qualified to.

Instructor

Discrete Structures
CS 173 at UIUC.
Intro to Algorithms & Models of Computation
CS 374 at UIUC.

Teaching Assistant

Discrete Structures
CS 173 at UIUC.
Intro to Algorithms & Models of Computation
CS 374 at UIUC.
Algorithms
CS 473 at UIUC.
Algorithms for Big Data
CS 498 ABD at UIUC.

*Rated excellent by my students. **Rated outstanding by my students. †Rated outstanding by the UIUC CS department.

Research

My work at Google involves distributed network design. My dissertation research was on structural and algorithmic aspects of surface-embedded graphs, which continues to be the subject of my personal research interest. In the past, I also worked on some problems in combinatorial optimization with a view towards learning theory.

Planar and Toroidal Morphs Made Easier
Coauthors Submitted to special issue of JGAA. Preliminary version appeared in GD 2021.
Download: GD, arXiv, pdf.

We present simpler algorithms for two closely related morphing problems, both based on the barycentric interpolation paradigm introduced by Floater and Gotsman, which is in turn based on Floater’s asymmetric extension of Tutte’s classical spring-embedding theorem.

First, we give a much simpler algorithm to construct piecewise-linear morphs between planar straight-line graphs. Specifically, given isomorphic straight-line drawings \(\Gamma_0\) and \(\Gamma_1\) of the same 3-connected planar graph \(G\), with the same convex outer face, we construct a morph from \(\Gamma_0\) to \(\Gamma_1\) that consists of \(O(n)\) unidirectional morphing steps, in \(O(n^{1+\omega/2})\) time. Our algorithm entirely avoids the classical edge-collapsing strategy dating back to Cairns; instead, in each morphing step, we interpolate the pair of weights associated with a single edge.

Second, we describe a natural extension of barycentric interpolation to geodesic graphs on the flat torus. Barycentric interpolation cannot be applied directly in this setting, because the linear systems defining intermediate vertex positions are not necessarily solvable. We describe a simple scaling strategy that circumvents this issue. Computing the appropriate scaling requires \(O(n^{\omega/2})\) time, after which we can can compute the drawing at any point in the morph in \(O(n^{\omega/2})\) time. Our algorithm is considerably simpler than the recent algorithm of Chambers et al. and produces more natural morphs.

A Note on Toroidal Maxwell–Cremona Correspondences
Preprint, September 2020.
Download: arXiv, pdf.
Abstract

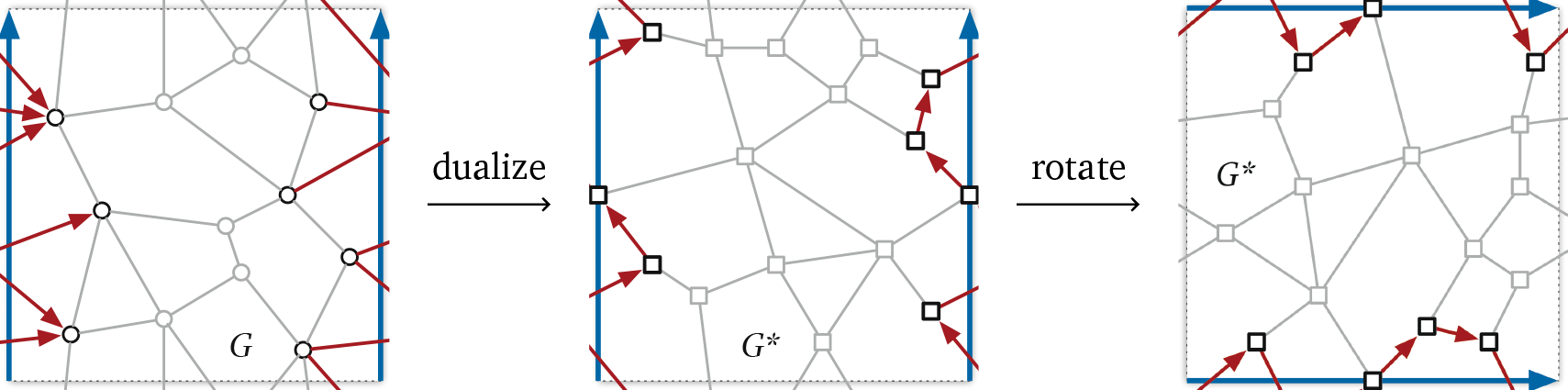
We explore toroidal analogues of the Maxwell–Cremona correspondence. Erickson and Lin showed the following correspondence for geodesic torus graphs \(G\): a positive equilibrium stress for \(G\), an orthogonal embedding of its dual graph \(G^*\), and vertex weights such that \(G\) is the intrinsic weighted Delaunay graph of its vertices. We extend their results to equilibrium stresses that are not necessarily positive, which correspond to orthogonal drawings of \(G^*\) that are not necessarily embeddings. We also give a correspondence between equilibrium stresses and parallel drawings of the dual.

How to Morph Graphs on the Torus
Coauthors Appeared in SODA 2021.
Download: SODA, arXiv, pdf. Presentation: SODA.
Abstract

We present the first algorithm to morph graphs on the torus. Given two isotopic essentially 3-connected embeddings of the same graph on the Euclidean flat torus, where the edges in both drawings are geodesics, our algorithm computes a continuous deformation from one drawing to the other, such that all edges are geodesics at all times. Previously even the existence of such a morph was not known. Our algorithm runs in \(O(n^{1+\omega/2})\) time, where \(\omega\) is the matrix multiplication exponent, and the computed morph consists of \(O(n)\) parallel linear morphing steps. Existing techniques for morphing planar straight-line graphs do not immediately generalize to graphs on the torus; in particular, Cairns’ original 1944 proof and its more recent improvements rely on the fact that every planar graph contains a vertex of degree at most 5. Our proof relies on a subtle geometric analysis of 6-regular triangulations of the torus. We also make heavy use of a natural extension of Tutte’s spring embedding theorem to torus graphs.

A Toroidal Maxwell–Cremona–Delaunay Correspondence
Coauthors Appeared in special issue of JoCG. Preliminary version appeared in SoCG 2020.
Download: JoCG, SoCG, arXiv, pdf. Presentation: VSAMRT.
Abstract

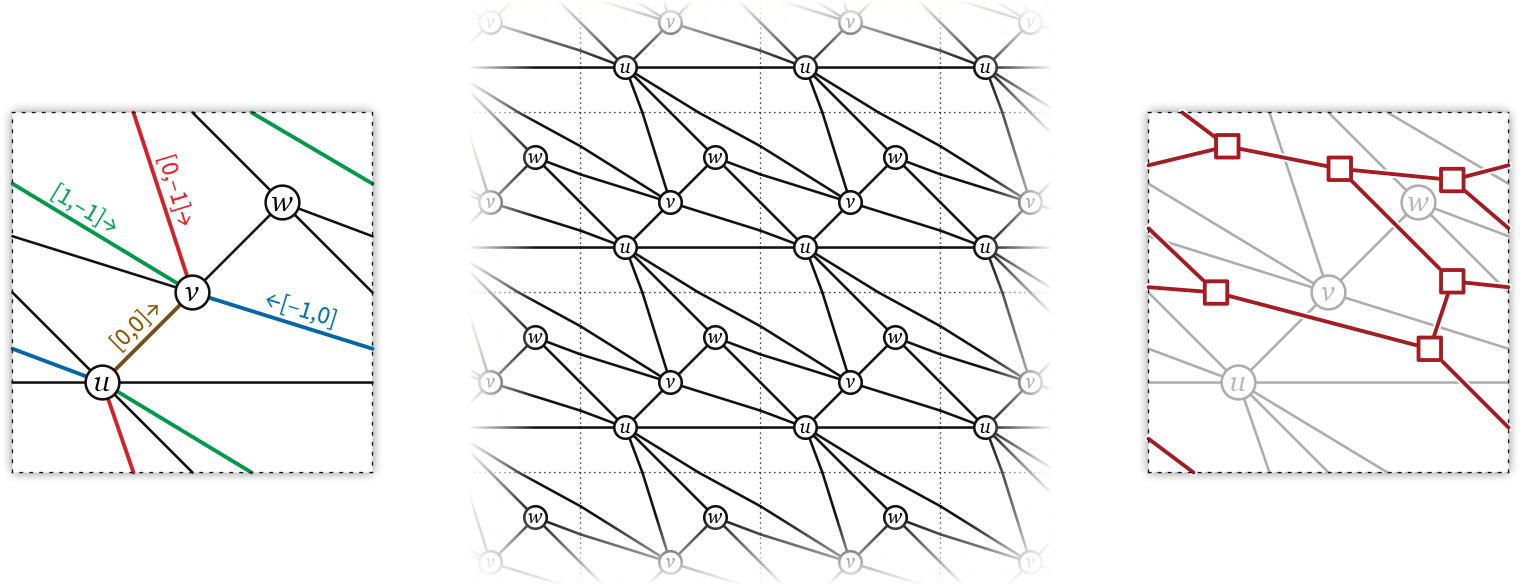
We consider three classes of geodesic embeddings of graphs on Euclidean flat tori:

  • A torus graph \(G\) is equilibrium if it is possible to place positive weights on the edges, such that the weighted edge vectors incident to each vertex of \(G\) sum to zero.
  • A torus graph \(G\) is reciprocal if there is a geodesic embedding of the dual graph \(G^*\) on the same flat torus, where each edge of \(G\) is orthogonal to the corresponding dual edge in \(G^*\).
  • A torus graph \(G\) is coherent if it is possible to assign weights to the vertices, so that \(G\) is the (intrinsic) weighted Delaunay graph of its vertices.

The classical Maxwell–Cremona correspondence and the well-known correspondence between convex hulls and weighted Delaunay triangulations imply that the analogous concepts for plane graphs (with convex outer faces) are equivalent. Indeed, all three conditions are equivalent to \(G\) being the projection of the 1-skeleton of the lower convex hull of points in \(\mathbb{R}^3\). However, this three-way equivalence does not extend directly to geodesic graphs on flat tori. On any flat torus, reciprocal and coherent graphs are equivalent, and every reciprocal graph is equilibrium, but not every equilibrium graph is reciprocal. We establish a weaker correspondence: Every equilibrium graph on any flat torus is affinely equivalent to a reciprocal/coherent graph on some flat torus.

Scenario Submodular Cover
Coauthors Appeared in WAOA 2016.
Download: WAOA, arXiv, pdf.
Abstract

Many problems in Machine Learning can be modeled as submodular optimization problems. Recent work has focused on stochastic or adaptive versions of these problems. We consider the Scenario Submodular Cover problem, which is a counterpart to the Stochastic Submodular Cover problem studied by Golovin and Krause (2011). In Scenario Submodular Cover, the goal is to produce a cover with minimum expected cost, where the expectation is with respect to an empirical joint distribution, given as input by a weighted sample of realizations. In contrast, in Stochastic Submodular Cover, the variables of the input distribution are assumed to be independent, and the distribution of each variable is given as input. Building on algorithms developed by Cicalese et al. (2014) and Golovin and Krause (2011) for related problems, we give two approximation algorithms for Scenario Submodular Cover over discrete distributions. The first achieves an approximation factor of \(O(\log Qm)\), where \(m\) is the size of the sample and \(Q\) is the goal utility. The second, simpler algorithm achieves an approximation bound of \(O(\log QW)\), where \(Q\) is the goal utility and \(W\) is the sum of the integer weights. (Both bounds assume an integer-valued utility function.) Our results yield approximation bounds for other problems involving non-independent distributions that are explicitly specified by their support.

Discrete Stochastic Submodular Maximization
Coauthors: Appeared in CIAC 2015.
Download: CIAC, arXiv, pdf.
Abstract

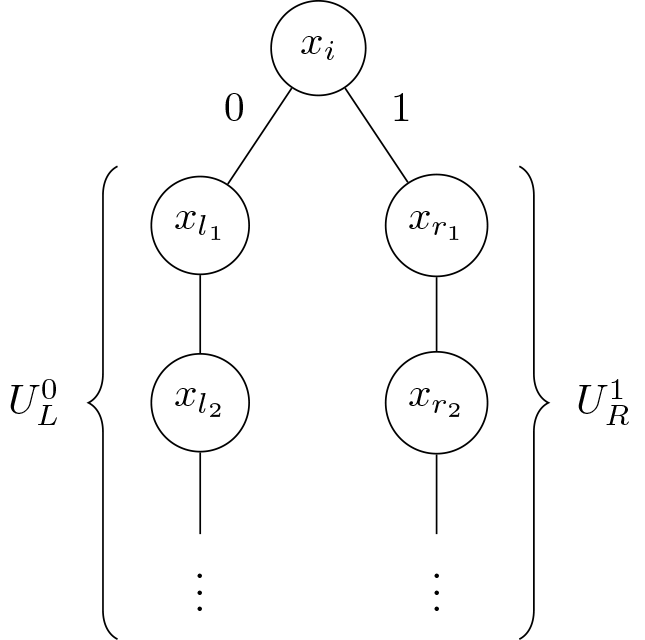
We consider the problem of stochastic monotone submodular function maximization, subject to constraints. We give results on adaptivity gaps, and on the gap between the optimal offline and online solutions. We present a procedure that transforms a decision tree (adaptive algorithm) into a non-adaptive chain. We prove that this chain achieves at least \(\tau\) times the utility of the decision tree, over a product distribution and binary state space, where \(\tau = \min_{i,j} \Pr[x_i = j]\). This proves an adaptivity gap of \(1/\tau\) (which is 2 in the case of a uniform distribution) for the problem of stochastic monotone submodular maximization subject to state-independent constraints. For a cardinality constraint, we prove that a simple adaptive greedy algorithm achieves an approximation factor of \((1−1/e^\tau)\) with respect to the optimal offline solution; previously, it has been proven that the algorithm achieves an approximation factor of \((1−1/e)\) with respect to the optimal adaptive online solution. Finally, we show that there exists a non-adaptive solution for the stochastic max coverage problem that is within a factor \((1−1/e)\) of the optimal adaptive solution and within a factor of \(\tau(1−1/e)\) of the optimal offline solution.

Expository Materials

I recently started writing a set of notes on Data Structures to supplement an improvised course I gave to W. Linda Xu. These notes are heavily incomplete and the presentation is not suitable for use by a more general audience (yet).

Basic Data Structures for an Advanced Audience
Download: draft pdf.

In the past I took notes live in LaTeX and then edited them afterwards. All notes are permanently in a draft state; some are more polished than others.

Combinatorial Optimization
as taught by Karthik Chandrasekaran in Fall 2015.
Download: draft pdf.
Intro to Cryptography
as taught by Oded Regev in Fall 2014.
Download: draft pdf.
Computational Complexity
as taught by Subhash Khot in Spring 2014.
Download: draft pdf.
Topology
as taught by Sylvain Cappell in Fall 2013, Spring 2014.
Download: draft pdf.

Miscellaneous Documents

Equilibrium Graphs on Flat Tori
PhD Dissertation.
Download: pdf.

Tutte's classical spring embedding theorem, and equilibrium graphs on the plane in general, have been a subject of study for many decades, with connections to and applications in many areas, including, but not limited to, discrete geometry, planar graph theory, graphics, surface parametrization, mechanical engineering, and graphical statics. In his 1963 paper, Tutte observed,

“[W]e may remark that very little is known about representations of graphs in the protective plane and higher surfaces.”

Six decades since Tutte's observation, however, our understanding of the properties and applications of equilibrium graphs on higher genus surfaces is still surprisingly limited, despite a growing body of work suggesting the utility of furthering this understanding.

In this thesis, we extend some existing structural properties and algorithmic applications of equilibrium graphs on the plane to the setting of flat tori. In particular, we consider the classical Maxwell–Cremona correspondence and a number of different planar morphing algorithms.

The Maxwell–Cremona correspondence, through a more modern computational geometry lens, can be summarized as stating that a planar graph is in positive equilibrium if and only if it is a weighted Delaunay graph of its point set. We derive some partial generalizations of this correspondence in the toroidal setting. In particular, we show that, whereas weighted Delaunay still implies positive equilibrium on flat tori, the converse is not always true; however, we give a full characterization of when the converse holds.

Next, we present generalizations of a few different techniques for morphing planar graphs. We show that techniques by Cairns and by Floater and Gotsman generalize to the toroidal setting with minor modifications; our generalization of the latter also provides a short proof of a conjecture of Connelly et al. for geodesic torus triangulations. On the other hand, Alamdari et al.'s improvement of Cairns' method uses techniques that do not seem to generalize. Instead, we obtain a similar improvement via a novel technique using toroidal spring embeddings, and then adapt said new technique to derive a new, simpler planar morphing algorithm.

Joke papers found below:

Need more RAM? Just invent time travel!
Coauthors: Appeared in SIGBOVIK 2019. April Fool's Paper. Winner of “Most frighteningly like real research” award.
Download: SIGBOVIK.
SMACK: when research in algorithms goes around in circles
Coauthors: Appeared in SIGBOVIK 2016. April Fool's paper.
Download: SIGBOVIK.

Music

I have performed in various choral groups for many years, usually as a tenor, occasionally as a baritone. I most recently sang with the University of Illinois Oratorio Society and the Baroque Artists of Champaign-Urbana (BACH).

Some pictures with groups I've sung with: BACH, NYU Madrigal Singers.

Very old recordings:

Crazy Little Thing Called Love
Collaborators: Listen: YouTube.
Fix You
Collaborators: Listen: mp3.
Shoshone Love Song
Collaborators: Listen: YouTube.